DUALIDAD EN PROGRAMACIÓN LINEAL

El dual es un problema de Programación Lineal que se obtiene matemáticamente de un modelo primal de Programación Lineal dado. Los problemas dual y primal están relacionados a tal grado, que la solución simplex óptima de cualquiera de los dos problemas conduce en forma automática a la solución óptima del otro. 

REGLAS DE OBTENCIÓN DEL DUAL

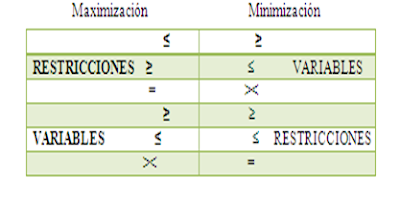
Si el modelo está escrito en la forma canónica, el dual resulta singularmente fácil de obtener. Por ejemplo, partiendo de la forma canónica del modelo de máximo.

Si se trata de obtener el dual del dual, se obtendrá el primal: se trata de una correspondencia biunívoca. De forma más general, las reglas para obtener el dual de cualquier modelo lineal se indican en la tabla adjunta.

INTERPRETACIÓN DE LAS VARIABLES DUALES

Cada variable del dual está asociada a una restricción del programa primal, y su valor óptimo representa el incremento de la función objetivo del primal por cada unidad que aumente el término independiente de dicha restricción, siempre que este último aumento no suponga un cambio de base. Es, por tanto, el precio adicional máximo que estamos dispuestos a pagar por el incremento del recurso. Los valores de estas variables se denominan precios sombra.

 

OBTENCIÓN DE LA SOLUCIÓN DEL DUAL

 El dual de un modelo lineal es otro modelo lineal, que puede solucionarse (después de las oportunas transformaciones, si alguna de las variables resultantes es no negativa o no restringida en signo), del Dualidad y análisis de sensibilidad en programación lineal59 mismo modo que el primal. Sin embargo, en general puede obtenerse la solución del dual resolviendo el primal. En los dos ejemplos siguientes, veremos dos modos de obtener la solución óptima del dual: 

 a) A partir de la tabla símplex óptima del primal,. La solución obtenida nos permitirá obtener un importante resultado: el teorema de la holgura complementaria.

 b)  Mediante un programa informático. Dado que en general los programas de resolución de modelos lineales realizan el análisis de sensibilidad, podemos realizar un análisis más exacto de la evolución de los precios sombra. Todo ello se muestra, con un modelo lineal sencillo.

DUAL  SIMÉTRICO

Los problemas duales simétricos son los que se obtienen de un problema primal en forma canónica y ‘normalizada’, es decir, cuando llevan asociadas desigualdades de la forma mayor o igual en los problemas de minimización, y desigualdades menores o igual para los problemas de maximización. Es decir, si el problema original es de la siguiente forma:

 

Máx Z(x) = ct x

s.a:

A x ≤ b

x≥ 0

El problema dual (dual simétrico) es:

MínG(λ) = λ b

s.a:

λA ≥ c

λ ≥ 0

Los restantes tipos de combinaciones de problemas, se conocen con el nombre de duales asimétricos. por ejemplo:

Máx Z(x) = ct x

s.a:

A x = b

x≥ 0

El problema dual (dual asimétrico) es

MínG(λ) = λ b

s.a:

λA ≥ c

λ >< 0, es decir, variables libres.

CARACTERÍSTICAS DE LAS SOLUCIONES DEL DUAL Y DEL PRIMAL

Si el primal tiene solución óptima acotada x*, el dual también tendrá solución óptima acotada u*.

a) Ambas soluciones darán el mismo valor de la función objetivo: c’· x* = b’ · u*

b) Si uno de los dos problemas tiene óptimo no acotado, el otro no tendrá solución (la región factible será un conjunto vacío).

                     RELACIONES PRIMAL-DUAL

Asociado a cada problema lineal existe otro problema de Programación lineal denominado problema dual (PD), que posee importantes propiedades y relaciones notables con respecto al problema lineal original, problema que para diferencia del dual se denomina entonces como problema primal (PP).

Las relaciones las podemos enumerar como siguen:

a) El problema dual tiene tantas variables como restricciones tiene el programa primal.

b) El problema dual tiene tantas restricciones como variables tiene el programa primal

c) Los coeficientes de la función objetivo del problema dual son los términos independientes de las restricciones o RHS del programa primal.

d) Los términos independientes de las restricciones o RHS del dual son los coeficientes de la función objetivo del problema primal.

e) La matriz de coeficientes técnicos del problema dual es la traspuesta de la matriz técnica del problema primal.

 

f) El sentido de las desigualdades de las restricciones del problema dual y el signo de las variables del mismo problema, dependen de la forma de que tenga el signo de las variables del problema primal  y del sentido de las restricciones del mismo problema. (Ver tabla de TUCKER)

g) Si el programa primales un problema de maximización, el programa dual es un problema de minimización.

h) El problema dual de un problema dual el programa primal original. 

TABLA TUCKER

DEFINICION DE TUCKER:

        

En programación matemática  las condiciones de Karush-Kuhn-Tucker (también conocidas como las condiciones KKT o Kuhn-Tucker) son condiciones necesarias y suficientes para que la solución de un problema de programación matemática  sea óptima. Es una generalización del método de Multiplicadores de Lagrange.

CONDICIONES DE KUNH-TUCKER EN DUAL SIMETRICO

TEOREMAS DE LA DUALIDAD

TEOREMAS DE EXISTENXIA

La condición necesaria y suficiente para que un problema de programación lineal tenga solución es que, tanto el conjunto de oportunidades del primal (S) como en conjunto de oportunidades del dual (S’) no sean vacíos, es decir, que ambos problemas sean factibles.

∃( x*, λ*) ←→S ≠0∧S’ ≠0

Corolario del teorema de existencia.

Una vez analizadas las condiciones que han de cumplirse para que exista solución optima, vamos a ver los diferentes casos

posibles:

a) S ≠0∧S’ ≠0 Ambos problemas tienen solución optima finita.

b) S =0∧S’ ≠O  El programa primal es infactible, y el programa dual es no acotado.

c) S ≠0∧S’ = 0   El programa dual es infactible, y el programa primal es no acotado.

d) S = 0 ∧S’ = 0 Ambos problemas son infactibles.

TEOREMAS DE DUALIDAD

La condición necesaria y suficiente para que exista solución óptima del primal ( x*), es que exista una solución óptima para el Dual ( λ*) y que valor de la función objetivo de ambos programas sea igual, es decir Z(x*) = G(λ*).

∃x*←→∃λ*/ Z(x*) = G(λ*) 

 TEOREMASDE HOLGURA COMPLEMENTARIA

La condición necesaria y suficiente para que (x*,λ*) sean soluciones óptimas del programa primal y dual, es que satisfagan las condiciones de holgura complementaria:

(c - λ*A) x*= 0

λ*( b - A x*) = 0 

Por su parte examinando el dual se encuentra que:

IMPORTANCIA DE LA DUALIDAD EN PROGRAMACIÓN LINEAL

La resolución de los problemas duales respecto a los primales se justifica dada la facilidad que se presenta dados problemas donde el número de restricciones supere al número de variables. Además de tener gran aplicación en el análisis económico del problema.

   Otra de las ventajas que presenta es que dado a que el número de restricciones y variables entre problema dual y primal es inverso, se pueden resolver gráficamente problemas que presenten dos restricciones sin importar el número de variables. 

VENTAJAS Y DE VENTAJAS DE LA DUALIDAD

 Ventajas

 Por una parte permite resolver problemas lineales donde el número de restricciones es mayor que  el número de variables. Gracias a los teoremas que expondremos a continuación la solución de unos de los problemas (primal o dual) nos proporciona de forma automática la solución del otro programa.

La dualidad permite realizar importantes interpretaciones económicas de los    problemas de programación lineal.

  La dualidad permite generar métodos como el método dual del simplex de gran importancia en el análisis de post- optimización y en la programación lineal para métrica.

Otra de las ventajas de la dualidad, es la posibilidad de resolver gráficamente algunos problemas.

Desventaja:

Una desventaja de este método, es que se requiere para empezar a iterar la condición de factibilidad dual.

ANÁLISIS SE SENSIBILIDAD

 El objetivo principal del análisis de sensibilidad es identificar el intervalo permisible de variación en los cuales las variables o parámetros pueden fluctuar sin que cambie la solución óptima.  Sin embargo, así mismo se identifica aquellos parámetros sensibles, es decir, los parámetros cuyos valores no pueden cambiar sin que cambie la solución óptima.  Los investigadores de operaciones tienden a prestar bastante atención a aquellos parámetros con holguras reducidas en cuanto a los cambios que pueden presentar, de forma que se vigile su comportamiento para realizar los ajustes adecuados según corresponda y evitar que estas fluctuaciones pueden desembocar en una solución no factible.

OBJETIVO DEL ANÁLISIS DE SENSIBILIDAD

El objetivo principal del análisis de sensibilidad es identificar el intervalo permisible de variación en los cuales las variables o parámetros pueden fluctuar sin que cambie la solución optima.  Sin embargo, así mismo se identifica aquellos parámetros sensibles, es decir, los parámetros cuyos valores no pueden cambiar sin que cambie la solución óptima.  Los investigadores de operaciones tienden a prestar bastante atención a aquellos parámetros con holguras reducidas en cuanto a los cambios que pueden presentar, de forma que se vigile su comportamiento para realizar los ajustes adecuados según corresponda y evitar que estas fluctuaciones pueden desembocar en una solución no factible.

ANÁLISIS DE SENSIBILIDAD: RESOLUCIÓN GRAFICA

El objetivo principal del análisis de sensibilidad es identificar el intervalo permisible de variación en los cuales las variables o parámetros pueden fluctuar sin que cambie la solución óptima.  Sin embargo, así mismo se identifica aquellos parámetros sensibles, es decir, los parámetros cuyos valores no pueden cambiar sin que cambie la solución óptima.  Los investigadores de operaciones tienden a prestar bastante atención a aquellos parámetros con holguras reducidas en cuanto a los cambios que pueden presentar, de forma que se vigile su comportamiento para realizar los ajustes adecuados según corresponda y evitar que estas fluctuaciones pueden desembocar en una solución no factible.

ANÁLISIS DE SENSIBILIDAD MEDIANTES PROGRAMAS INFORMÁTICOS

Los programas informáticos que resuelven modelos de programación lineal, como el LINDO, suelen incorporar la posibilidad de realizar el análisis de sensibilidad de los coeficientes de coste c y de los términos independientes de las restricciones b. el resultado de este análisis es el intervalo de valores de estos parámetros para el que se mantiene la base. Vemos como muestra el programa lindo los resultados del análisis de sensibilidad.

Resolución mediante el programa LINDO del modelo lineal:

MAX       20P1 +   60P2

ST

HH)         30P1 +   20P2    <2700

HM)        5P1    +   10P2     <850

PM)         P1     +    P2         >95

    END

IMPORTANCIA DEL ANÁLISIS DE SENSIBILIDAD

La importancia del análisis de sensibilidad se manifiesta en el hecho de que los valores de las variables que se han utilizado para llevar a cabo la evaluación del proyecto pueden tener desviaciones con efectos de consideración en la medición de sus resultados.

La evaluación del proyecto será sensible a las variaciones de uno o más parámetros si, al incluir estas variaciones en el criterio de evaluación empleado, la decisión inicial cambia. El análisis de sensibilidad, a través de los diferentes modelos, revela el efecto que tienen las variaciones sobre la rentabilidad en los pronósticos de las variables relevantes.

 

ÁNEXOS

VIDEO PROBLEMA  DUAL

VIDEO ANALISIS DE SENSIBILIDAD